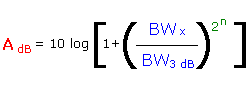
Figure 1 - Butterworth narrow band filter attenuation formula
LAST MODIFIED:
Narrow band filters are filters where the fractional bandwidth is extremely small in a relative sense. My personal definition of a narrow band filter is where the narrow band filter has a fractional bandwidth NOT exceeding 1%. These filters can be adapted to become fixed or tunable antenna pre-selector filters.
A filter with a bandwidth of 200 Khz ( ± 100 Khz ) centred around 7100 Khz would represent a bandwidth of about 2.86%
As just one example of a narrow band filter for the front end of a receiver I'll look at a double tuned front end filter for a single frequency receiver built to receive WWV or VNG time signals at 5000 Khz. These are amplitude moduated ( AM ) signals with modulation not exceeding 1000 Hz. Strictly speaking all we want to receive is around 4999 Khz to 5001 Khz, that is only a 2 Khz bandwidth. Technically it is quite feasible to construct a crystal filter to do this job but that is not the subject of our discussion here.
A single channel superhetrodyne receiver operating at 5000 Khz would normally have an IF (Intermediate Frequency - where all the real amplification takes place) of the standard 455 Khz.
Ceramic narrow band filters are available for use at 455 Khz and my personal preference for AM reception is ± 3Khz including shortwave reception. Clearly our main selectivity is at the IF of 455 Khz. Let's get back to our front end filter, how wide should it be?
In a superhetrodyne receiver operating at 5000 Khz and with an IF of 455 Khz the local oscillator would be 5000 Khz ± 455 Khz. The LO is going to be either 5455 Khz or 4545 Khz. We will only consider the example of 5455 Khz because you can apply the same principles to the other frequency of 4545 Khz.
With a LO of 5455 Khz and an IF of 455 Khz our receiver can only respond equally well to two distinct frequencies, here I'm deliberately ignoring spurious responses called "spurs". The two frequencies are 5455 Khz ± 455 Khz = 5000 Khz and 5910 Khz.
The 5000 Khz is the desired frequency whilst the 5910 Khz frequency is called the "mirror image" or image frequency and this is the one we MUST remove. This is the ONLY reason we have a narrow band filter for our WWV or VNG 5Mhz front end.
For our narrow band filter for the WWV or VNG 5Mhz front end I am going to use, for simplicity sake, a double tuned "Butterworth narrow band filter". Simplicity in the sense of easy to design, construct AND align.
First let's look at the steepness factor we need to look at, if our ideal bandwidth is ± 3 Khz around 5000 Khz and the extreme is ± 910 Khz around 5000 Khz then we have a steepness factor of 910 / 3 = 303. Consulting some filter tables I can determine that for a double tuned narrow band filter of n = 2 the attenuation for a steepness factor of 10, the limit of my table, is 40 dB. If you studied the topic decibels you would know that -40 dB is a sgnificant power reduction. It is a voltage attenuation of -100.
All this means for our Butterworth narrow band filter is if our steepness factor exceeds 10, we will achieve at least 40 db attenuation.
However I am greedy, I really want an attenuation factor of 60 db. For the ignorant who haven't studied decibels, that is NOT an increase of 50%. In voltage reduction it is -1,000 or a ten fold increase and in power terms a 100 times increase. Because my table does not extend beyond a steepness factor of 10 I'm going to use the following classy formula to calculate the necessary bandwidth to achieve my desired 60 dB attenuation to the unwanted 5910 Khz signal.
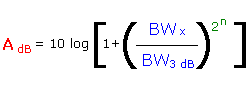
Figure 1 - Butterworth narrow band filter attenuation formula
Now so you understand what is happening here we will use a worked example, in fact I'll do two worked examples. Adb is the attenuation which results, 10 log for those who know decibels is 10 times the log of the amount determined between [ and the ] brackets. BWx is the highest frequency and BW3dB is the 3 dB bandwidth. The n is the number of resonators we're using, in our case for a double tuned narrow band filter, n = 2.
I said my tables say a steepness factor of 10 = at least a 40 dB attenuation. How about we check that one out? Follow this:
BWx / BW3dB = 10 and 2n = 2 X 2 = 4. Looking at the formula and following the order for algebra "BODMAS" ( inside brackets, outside brackets, division, multiplication, addition and subtraction ) we get 10 / 1 = 10, then plus 1 = 11 all of which is raised to the power, "Yx" of 2 X 2 = 4 results in 14,641 the log of which is 4.166 which is then multiplied by 10 to give us an Adb attenuation factor of 41.66 dB. Piece of cake!
All right I'm greedy, I want 60 db. Working backwards 60 / 10 = 6 and anti-log 6 = 1,000,000 (incidently that is why there are 6 zeros). Here is gets somewhat tricky, on my calculator I have 1,000,000 entered and THEN I press the "second function" key, THEN the "Yx", ENTER 4 to get an answer of 31.62227766 ( trivia - this answer incidently is exactly the square root of 1,000 ). This answer is the required steepness factor BWx / BW3dB. If our desired 3 db bandwidth is 3 Khz then we can make our 60 dB bandwdth = 3 X 31.62 or say ± 100 Khz. For the purists among you ± 94.868 Khz.
Very long winded? Yes but much better than "monkey see - monkey do" principle. You should now be able to design any Butterworth narrow band filter to suit any achievable design goal and know exactly why you have arrived at your answers. So our Butterworth narrow band filter now has an overall bandwidth of 200 Khz.
Centre frequency is 5000 Khz, design bandwidth is 200 Khz therefore 5000 / 200 = 25 (QBw) which is then mutiplied by 1.414 (Qn)for a two pole filter, this also happens to be the square root of 2. So 25 X 1.414 = 35.35 - see later the figures for using 3 to 5 pole resonators

Figure 2 - Butterworth narrow band filter
In figure 2 I have depicted a two pole ( two resonators L1 / C2 and L2 / C4) Butterworth narrow band filter coupled by C3 which is critical in determining the filter bandwidth. C1, C5 are respectively coupling capacitors used simply to match the filter impedance back to the input impedance Zin and output impedance Zout. All we have to do is determine the required values of L and C.
BASIC CALCULATIONS:
1. Filter impedance ( Z ) = Qn X QBw X 2 X pi X Fo X L
2. LC = 25330.3 / ( Fo X Fo ); where Fo is in Mhz
3. Co = LC / L
4. C3 = Co X [0.707 / ( Qn X QBw )]
5. C2 = Co - C1 - C3
6. C4 = Co - C3 - C5
The calculations for C1 and C5 and other options I will deal with shortly.
Why did I jump ahead here straight to C3 and Co? Because if you proceed with calcuations in the classic fashion you often finish up with impractical values for C3 such as 0.348 pF. I might show you later how to achieve such values however, I strongly recommend selecting a "real world" practical value for C3. Here we will initially select a value of 4.7 pF which I prefer to call 4p7, note the "p" in place of the decimal point? A superior system.
If C3 = 4p7 then using algebra from calculation 3 above where I said C3 = Co X [0.707 / ( Qn X QBw )] it follows by filling in known values 4p7 = Co X [0.707 / ( 1.414 X 25 )]
Re-arranging to solve for the unknown (high school algebra WAS a waste of time?), we now get Co = 4p7 / ( 0.707 / 35.35 ) = 235 pF
Looking at calculation 2 above we find at 5 Mhz, LC = 25330.3 / ( Fo X Fo ) = LC = 25330.3 / ( 5 X 5 ) = 25330.3 / 25 = 1013.2
If LC is 1013.2 and we calculated Co as 235 pF then L the inductance must be 1013.2 / 235 = 4.31 uH
Knowing L is now 4.31 uH and using calculation 1 above, our filter impedance is Z = Qn X QBw X 2 X pi X Fo X L which means Z = 1.414 X 25 X 2 X 3.1416 X 5 X 4.31 = 4786 ohms
Because in my example for the WWV/VNG receiver I'm going to use a short whip antenna about 600 mm (2') long and the filter is going to be followed by a buffer amplifier of known input impedance, I'll proceed as follows:
My 600 mm whip antenna has an approxmate capacitance of around 15 pF. With whip antennas assume a ball park figure of 25 pF per metre length. If you did the tutorial on reactance you would know that the 600 mm whip capacitance of 15 pF represents an impedance at 5 Mhz of around 2122 ohms.
Now we have to calculate a value of C1 which transforms the filter impedance of 4786 ohms back to the whip source impedance of 2122 ohms. The formula for calculating the "reactance" of C1 is:
Xc = SQRT [ Zfilt X Zin - ( Zin X Zin ) ] = SQRT [ 4786 X 2122 - ( 2122 X 2122 ) ] = SQRT [ 5653008 ] = 2378 ohms
A reactance of 2378 ohms at 5 Mhz is a capacitor of 13.38 pF. I would use a 12 pf capacitor for C1 in the "real world" because the input impedance of 2122 ohms was at best a "guesstimate". We proceed the same way for the terminating impedance where I'm going to use the amplifier depicted in figure 1 in the broad band amplifiers tutorial. Here the input impedance was defined as 1000 ohms, or whatever value I wanted. Therefore C5 calculates as:
Xc = SQRT [ Zfilt X Zin - ( Zin X Zin ) ] = SQRT [ 4786 X 1000 - ( 1000 X 1000 ) ] = SQRT [ 3786000 ] = 1946 ohms
A reactance of 1946 ohms at 5 Mhz is a capacitor of 16.36 pF. I would use two 8.2 pF ( 8p2 ) capacitors in parallel for C5 ( 2 X 8.2 = 16.4 pF ) because the input impedance of 1000 ohms for the amplifier was pretty wel defined.
Earlier I stated:
5. C2 = Co - C1 - C3
6. C4 = Co - C3 - C5
Therefore C2 = Co - C1 - C3 = 235 - 12 pF - 4p7 = 218.3 pF. I would use a 180 pF capacitor with a 50 pF trimmer in parallel for tuning purposes. Smilarly C5 = 235 Pf - 4p7 - 16.4 = 213.9 pF. Again a 180 pF capacitor with a 50 pF trimmer.
The inductor NEEDS to have an unloaded Q ( Qu ) at least several times higher ( X 5 ) than design Q to avoid costly insertion losses. I would use a T50-6 toroid for L1 and L2 to achieve high "Q".
Obviously that is only one set of calculations, the possible answers for designing Butterworth narrow band filters is infinite. If those values didn't suit you then change the value of C3 in your Butterworth narrow band filter or start out with an inductor of your choice.
Finally REMEMBER any filter must be terminated, preferably doubly, in design impedances. In my example the buffer amplifier input resistor of 1,000 ohms provided the necessary termination and C5 provided the transformation back to the filter impedance of 4,786 ohms. C3 determines the bandwidth. Any filter improperly terminated will NOT perform as expected.
If I get sufficent response to justify the efforts I will extend this interesting topic futher. This page comprises nearly 2,000 words and that's a big effort.
band pass filters
filter software
high pass filters
if amplifier filters
low pass filters
decibels
reactance
resonance
"Q"
toroids
superhetrodyne receivers
broad band amplifiers
join our "electronics discussion group"
NEW! - How to link directly to this page
Want to create a page link to me from your site? It couldn't be easier. No HTML knowledge required; even the technophobes can do it. All you need to do is copy and paste, the following code. All links are greatly appreciated; I sincerely thank you for your support.
Copy and paste the following code for a text link:
and it should appear like this:
<a
href="https://www.electronics-tutorials.com/filters/narrow-band-filters.htm" target="_top">visit VK2TIP's Narrow Band Filters Page</a>
visit VK2TIP's Narrow Band Filters Page
the author Ian C. Purdie, VK2TIP of www.electronics-tutorials.com asserts the moral right to
be identified as the author of this web site and all contents herein. Copyright © 2000, all rights reserved. See copying and links.
These electronic tutorials are provided for individual private use and the author assumes no liability whatsoever for the application, use, misuse, of any of these projects or electronics tutorials that may result in the direct or indirect damage or loss that comes from these projects or tutorials. All materials are provided for free private and public use.
Commercial use prohibited without prior written permission from www.electronics-tutorials.com.
Copyright © 2000, all rights reserved. URL - https://www.electronics-tutorials.com/filters/narrow-band-filters.htm
Updated 29th December, 2000